Gradient-based Particle Swarm Optimization for Identifing drug combination

This is a literature review and demonstration of what I did for futures works based on this study.

Recently I read a interesting article that demostrated how Particle Swarm Optimization(PSO) provide a efficient method to infer unknown parameters in traditional Mass Action model. This paper specifically focused on IGFR-1 signaling network. The grandiose context of this research aims to investigate the complex dynamic network by which targeted drugs affect multiple targets.

Biological Background and Method:

The biological system studied in this research is insulin-like growth factor (IGF-1) signaling network in the MDA-MB231 breast cancer cell line. The IGF system is associated with tumorigenesis and proliferation , survival and migration of tumor cells. More specifically, the insulin-like growth factor (IGF-1) is an omnipresent multifunctional tyrosine kinase(Bartucci), which is highly related to the growth of breast cancer cells.

A previous study of invasion of MDA-MB-231 BrCa cells disclosed that IGF-1 induced formation of cellular protrusions to serve as an impetus of the cell to pull forward during migration(Christopoulos). Furthermore, dual therapies targeting this signaling network ( IGF1R, PI3K, m-TOR, and MEK) in the MDA-MB-231 cell line, were corroborated in vitro that is possible to halt reactivation of these tyrosine kinase pathways and reduce toxicity with administration of low doses(Ayunadirah). Those pre-clinical findings encourage scientists to investigate IGF-1 signaling network in order to discover new therapeutic for breast cancer. Another motivation to build this network is that the experimental data is enormous and comprehensive. This is a prerequisite for building a trustworthy network and offers the possibility of performing experimental tests. Moreover, several clinical trials of breast cancer therapy are also based on this signaling network components, so it has great clinical applicability.

The specificity of current drugs has a considerable drawback: Bypass mechanisms and activation of regulatory loops can offset the effects of inhibiting a target protein alone. Thus, it is essential to utilize advancement of computational modeling driven by mathematical and statistical theorems to predict how individual component contribute to the entire biological network. This work presented an optimized IGF-1 training model that predicts how targeting a single signaling protein fluctuates the rest of the network and identifies drug combinations that reduce phosphorylation of other proteins in the network.

The overall idea of developing this computational model is combining the traditional mass action model with particle swarm optimization. The model as was trained with the experimental data and deduce the unknown parameters. The unknown parameters usually are the kinetic rate constants and the initial concentrations of the proteins. The reason to use mass action modeling is that it is a consensus strategy applied on activation and inhibition mechanisms of proteins. Meanwhile, the Particle swarm optimization (PSO) is a kind of algorithm with simple concept, easy implementation and robustness to parameters ( K. Y. Lee). It improves the non-effective intervention strategies and efficient than simulating multiple target annealing intervention. The PSO follows the iterative updating rules as shown below:

Where the ω is the inertia factor; r1 and r2 are two random numbers uniformly distributed in the interval [0,1]; and c1 and c2 are the coefficients of self-recognition and social component. The particle position xij is representing the unknown parameters in mass action model. The particle velocity vij indicates the degree to which the parameter values change iteratively. Particle fitness is defined as the distance between the experimentally and computationally measured time-course protein data.

Issues, Limitations, Critiques:

From author notes, this article is focused on inhibition of the MAPK and PI3K / Akt pathway. Several other kinases and pathways may regulate the activity of MDA-MB231 cells, but the experimental results showed that simultaneous inhibition of the MAPK and PI3K / Akt pathways was sufficient to significantly decrease cell proliferation. From my point of view, the system choice in this research is intelligent since there are 6 molecules can be assayed, and the experimental database is sufficient to decrease the random errors. The optimal algorithm chosen, which is PSO, uses individual and group experiences to search the optimal solutions. Nevertheless, previous solutions may not provide the solution of the optimization problem. Thus, the speed of this non-gradient method would slower than gradient optimization. Another concern is about database management. PSO can’t handle big biological data because the amount of computation increases exponentially with increasing data dimensions. However, because of the limited number of experimental trials, human labor, and funding reasons, it is possible that the current database size can be adapted with such algorithms.

Thoughts of “Path forward” in this study

In order to speed up PSO, we propose to expedite the convergence near the neighborhood of local solution by applying gradient descent scheme(GPSO). We will estimate the neighborhood of local solutions approximately by means of traditional PSO, then the gradient-descent method further facilitates efficient searching for the best local minimum.By this way, the GPSO is able to locate global optimal solutions with these delicate and efficiently calculated local solutions. Moreover, to overcome the drawbacks of overlapping selections in random sampling in GPSO, we will additionally involve Latin hypercube sampling(LHS) for random initialization. In each current iteration of LHS, the randomized initiation points remember their positions in each dimension so the repeated initiation points won’t occur in the next search. The dimensions of this LHS are dependent on unknown parameters from the mass action model. We also consider our variable boundary conditions in this GPSO algorithm. As our particle represent the kinetic constant and initial concentrations, we adding penalty term in the cost function to call off the negative values searching.

Gradient-based Particale Swarm Optimization(GPSO)

Methods

Compensation methods for missing experimental Data:

One challenge of this study is that the I wasn’t able to obtain experimental data to train the optimization model. The RPPA results of 6 read-out molecules from the original paper involve vast sets of ODEs that take immense time to train. In order to save time, two methods to compensate for the training set absence were implemented to generate alternative experimental results from RPPA. The initial attempt is randomly selecting data points within the range of real RPPA data, however, it rose the potential risk that the randomized data point may not follow or even critically deviate from the biological observations. To ensure the training set is capable to represent real biological data, the results of the mass action (MA) model with known parameters solved by traditional PSO were used as primary synthetic training data. Noisy was randomly added to this training data set to enhance the robustness of the model. Then, those known parameters were treated as unknown parameters which were described by particle positions in GPSO. In this way, the GPSO was further tested to see if it could restore the results of known parameters.
Fifty time units (Swarm Size) were chosen to solve the 3 ODEs. Traditional PSO was applied following the equations(eq. 1), where all the non-random coefficients were set to default values. r1 and r2 were two random numbers uniformly distributed in the interval [0,1], selected by means of Latin Hypercube Sampling with Matlab built-in function lhs(). The global best particle located by traditional PSO was then served as a starting point for gradient descent(eq.3) to be executed elaborative and rapid local research to obtain a precise local minimum.

The step size η was set equal to 0.1 and k represents the current iteration number of local research.The cost function here was the SD-Weighted Error between experimental data yijm and predictive data(eq.4). The gradient was calculated with respect to the results from mass action modeling.Once the gradient descent produced local optimization, the results would feedback to the traditional PSO as the global best solution to proceed next iteration. Through this hybrid optimization process, the traditional PSO employed the accurate global optimization founded by rapid gradient descent to move forward in each iteration.

Results

Figure below displayed GPSO training results with biased experimental data. The species X1, X2, X3 represented IGF, IGFR, and activated IGFR*. The Quasi-state assumption was made that species except these three proteins stayed at steady-state with their initial concentrations. The red dots were the synthetic noisy experimental data from the MA model with traditional PSO inferred parameters. The X1 dropped fast initially and tend to remain at a low level. A similar trend in the blue solid line showed protein level from the MA model with GPSO inferred parameters. It confirmed that GPSO is capable to restore traditional PSO results with limited variability and further demonstrated its ability to search unknown parameters in the real biological networks.

As the large deviation of the randomly generated training set, the biased experimental data was then adopted as the main training data to train the GPSO. The capability of efficiently searching optimization solutions within short-time and long-time was examed for both PSO and GPSO. The following figures displayed a comparison of PSO and GPSO within short-term Monte Carlo simulations (100 Iterations) and long-tern Monte Carlo simulations(2500 Iterations). It confirmed that GPSO improved the efficiency of traditional PSO as it took fewer iterations to arrive same error level compared to PSO. It also convinced that the GPSO contributed more accurate results, independent of the total amount of iterations.

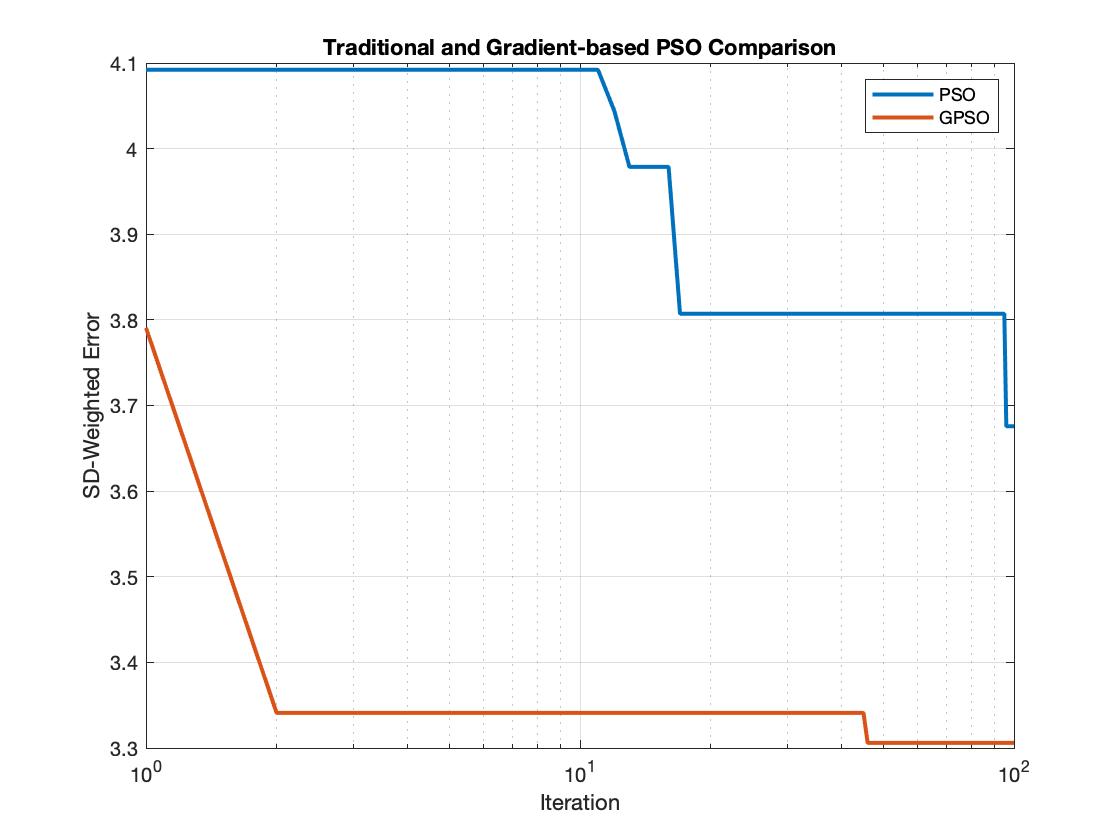
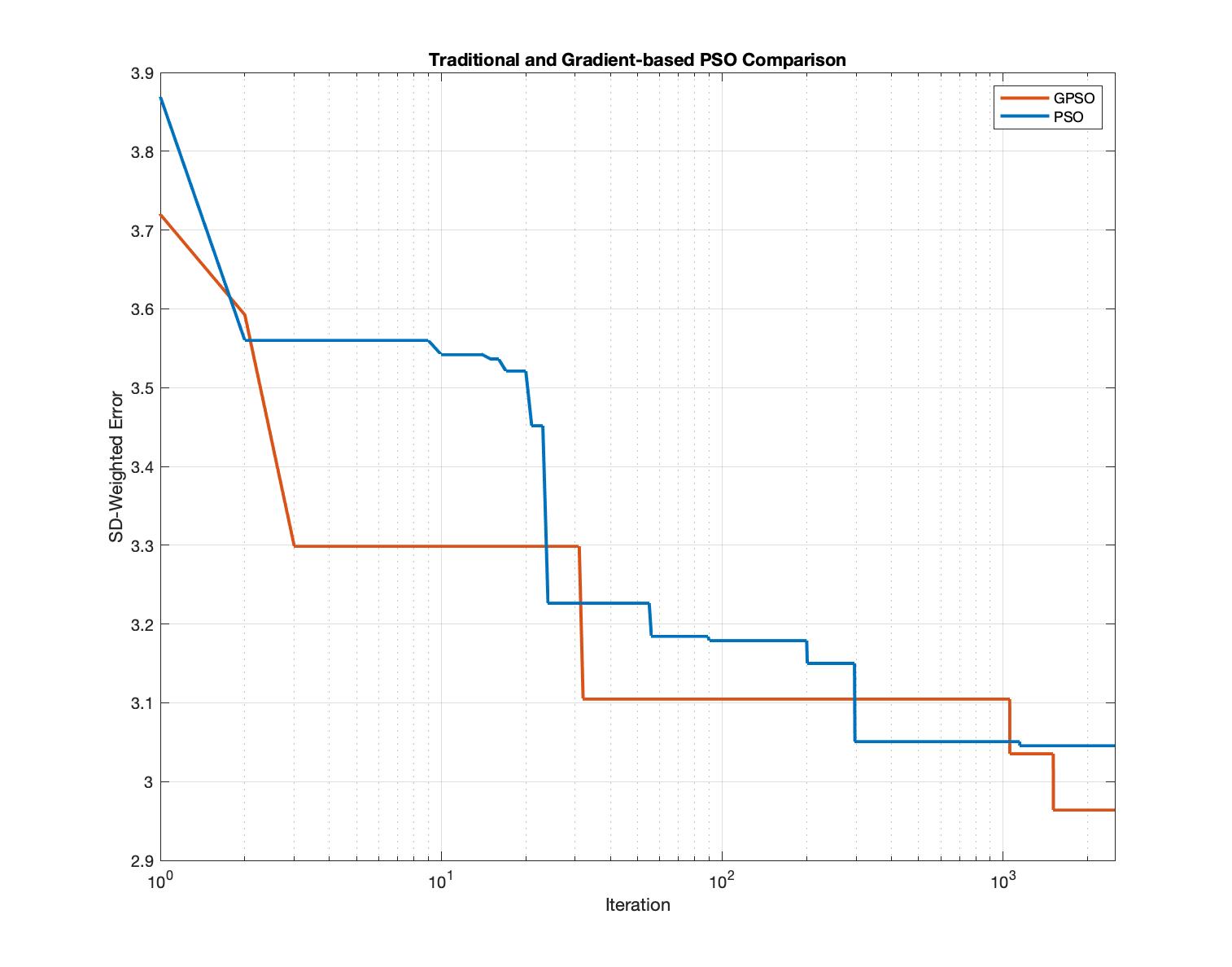
Conclusion:

By completed this aim, the GPSO was proven its strength to fetch a more accurate global solution with fewer iterations. Traditional PSO is a stochastic optimization algorithm to perform global optimization but is likely spending extra computational effort doing a random search even it is closed to the local solution. Deterministic algorithms like gradient descent can overcome the drawbacks of the stochastic process which is able to converge rapidly but may get trapped in the local minima for multimodal functions. The GPSO combining the advantages of stochastic and deterministic optimization schemes but avoids their weaknesses is of interest. With low-dimensional training data, GPSO provides a novel method to facilitate Mass Action modeling in the different networks in various cell lines. It also inspires computational mathematicians and biologists to develop future therapeutics driven by the insights of the complex biological responses.

Limitation and Path forward for GPSO:

Due to the limited time and computational resources, only a small motif of the IGFR-1 network was tested by GPSO. Species outside of the motif were assumed to be at a steady state, which possessed the restrained ability to handle large amounts of parameters. In a real network, the complexity of biological responses is way higher, thus, broadening the modeling network is necessary. This study proved the capability of GPSO efficiently and accurately infer single unknown parameters, however, multivariable GPSO needs to be constructed to be able to solve more complex networks.

References:

• Bartucci M, Morelli C, Mauro L, Andò S, Surmacz E. Differential insulin-like growth factor I receptor signaling and function in estrogen receptor (ER)-positive MCF-7 and ER-negative MDA-MB-231 breast cancer cells. Cancer Res. 2001 Sep 15;61(18):6747-54. PMID: 11559546 .
• Morimura S, Takahashi K. Rac1 and Stathmin but not EB1 are required for invasion of breast cancer cells in response to IGF-I. Int J Cell Biol. 2011;2011:1–9.
• Christopoulos, P.F., Msaouel, P. & Koutsilieris, M. The role of the insulin-like growth factor-1 system in breast cancer. Mol Cancer 14, 43 (2015). https://doi.org/10.1186/s12943-015-0291-7
• Ayunadirah Ayub, Wai Kien Yip, Heng Fong Seow, Dual treatments targeting IGF-1R, PI3K, mTORC or MEK synergize to inhibit cell growth, induce apoptosis, and arrest cell cycle at G1 phase in MDA-MB-231 cell line, Biomedicine & Pharmacotherapy,Volume 75, 2015, Pages 40-50, ISSN 0753-3322, https://doi.org/10.1016/j.biopha.2015.08.031.
• K. Y. Lee and J. Park, “Application of Particle Swarm Optimization to Economic Dispatch Problem: Advantages and Disadvantages,” 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 2006, pp. 188-192, doi: 10.1109/PSCE.2006.296295.
• Noel, Mathew M. “A New Gradient Based Particle Swarm Optimization Algorithm for Accurate Computation of Global Minimum.” Applied Soft Computing, vol. 12, no. 1, 2012, pp. 353–359., doi:10.1016/j.asoc.2011.08.037.